
Use the time formula and find the time taken by the cyclist in covering the distance.Īnswer: The time taken by the cyclist to cover 20 km at 5km/hr is 4 hours.Įxample 3: Using the time formula calculate the time taken by a person in covering a distance of 400 kilometers at speed of 20 kilometers per hour? Using the time formula calculate the time taken by the train in covering the distance.Īnswer: The time taken by the train to cover 120 km at the speed of 60km/hr is 2 hours.Įxample 2: A cyclist covers 20 km at a speed of 5km/hr. Let us solve some interesting problems using the time formula.Įxample 1: A train covered a distance of 120 km at a speed of 60km/hr.
#Physics calculator period trial
With Cuemath, find solutions in simple and easy steps.īook a Free Trial Class Examples Using Time Formula Use our free online calculator to solve challenging questions.
#Physics calculator period how to
Let's take a quick look at an example showing how to use the formula for time.Įxample: What will be the total time to cover 3600 m at 2 meter per seconds?Īnswer: Total time taken to cover the distance of 3600 m is 1800 seconds. Time formula can be used to find the time taken by an object, given the distance and unit speed.
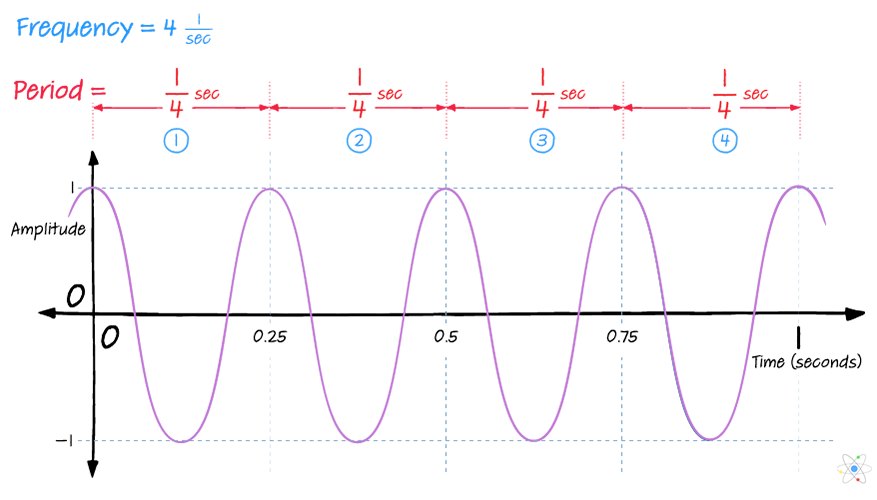
The Formula of Time of a given body can be expressed as, This progression is in such a manner that it goes from the past to the present and finally into the future. Time refers to the progression of events. Time formula can be defined as the ratio of distance covered by an object to a unit speed. The SI unit of time is s. Let us study the formula of time using some solved examples. For the physical pendulum with distributed mass, the distance from the point of support to the center of mass is the determining "length" and the period is affected by the distribution of mass as expressed in the moment of inertia I.The formula of time helps in calculating the time taken by an object to travel a certain distance at a given speed. The period of a simple pendulum for small amplitudes θ is dependent only on the pendulum length and gravity. In which case Newton's 2nd law takes the formĮven in this approximate case, the solution of the equation uses calculus and differential equations. When displaced from its equilibrium point, the restoring force which brings it back to the center is given by:įor small angles θ, we can use the approximation The frequency of the pendulum in Hz is given byĪ point mass hanging on a massless string is an idealized example of a simple pendulum. Which is the same form as the motion of a mass on a spring: The anglular frequency of the motion is then given by The motion of a simple pendulum is like simple harmonic motion in that the equation for the angular displacement is The size of the oscillations - how far the pendulum swung back and forth - didn't affect the frequency of those oscillations." He found something interesting: The number of heartbeats between swings of the chandelier was roughly the same, regardless of whether the swings were wide or narrow. Intrigued, Galileo decided to measure how much time it took for each swing, using the only approximately periodic event to which he had ready access: the beating of his own pulse. The chandelier overhead would swing gently back and forth, but it seemed to move more quickly when it was swinging widely (after a gust of wind, for example) and more slowly when it wasn't moving as far. "In 1581, a young Galileo Galilei reportedly made a breakthrough discovery while he sat bored during a church service in Pisa. Sean Carroll relates the story of Galileo's discovery of the fact that for small amplitudes, the period and frequency are unaffected by the amplitude. If the rod is not of negligible mass, then it must be treated as a physical pendulum. This expression for period is reasonably accuratefor angles of a few degrees, but the treatment ofthe large amplitude pendulum is much more complex. Note that the angular amplitude does not appear in the expression for the period. (Enter data for two of the variables and then click on the active text for the third variable to calculate it.) For small amplitudes, the period of such a pendulum can be approximated by: It is a resonant system with a single resonant frequency.

A simple pendulum is one which can be considered to be a point mass suspended from a string or rod of negligible mass.


 0 kommentar(er)
0 kommentar(er)
